
When working with MoGraph, one of the most common creative needs is precise control over how clones animate in sequence. The default Linear Field gives you spatial control, but sometimes you don’t want the animation to depend on the physical layout of the clones — you want it to be driven by index order, especially in setups where clones are arranged irregularly, scattered, or dynamically generated.
This is where the Sequential MoGraph Field script becomes invaluable.
What This Field Does
This custom Python Field lets you animate clones strictly by clone index, rather than by world-space bounding box. That means:
- Clone 0 animates first
- Clone 1 animates second
- Clone 2 animates third
- …and so on
No matter how your clones are positioned, rotated, randomly offset, or distributed, the animation progression always follows the clone order generated by the Cloner.
This is extremely powerful for controlled, art-directed motion that must follow a specific reveal order, timing pattern, or step-based structure.
Why This Is Useful for Motion Designers
1. Order-Based Reveals Without Layout Limitations
Great for designs where clones may be arranged in circular, spherical, scattered, grid, or completely random rigs — but still need a clean sequential animation.
Example uses:
- Revealing hundreds of icons or logos one by one
- Animating modular pieces of a complex object assembly
- Triggering elements in a UI animation
- Creating timed “wave” animations along the clone order
2. Perfect Temporal Control: Steps, Overlap, Delay
The script includes:
- Steps (multi-phase animation)
- Overlap (blend between steps)
- Delay (per-clone staggering)
- Randomness (natural motion variation)
This gives you the kind of timing control usually found in high-end particle animation systems.
3. Works With Any MoGraph Setup
Because the script ignores bounding boxes, it works identically in:
- Linear Cloners
- Radial Cloners
- Grid Arrays
- Multi-Cloner hierarchies
- Fracture objects
- Dynamic or animated clone arrangements
Your animation logic stays consistent even if the layout is modified later.
4. Consistent Falloff Behavior
The field uses a normalized sequential falloff that behaves like a Linear Field but in index space. This keeps transitions clean and predictable.
How to Use
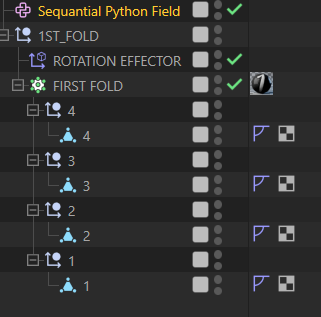
- Add a Python Field to your setup.
- Paste the script into the field.
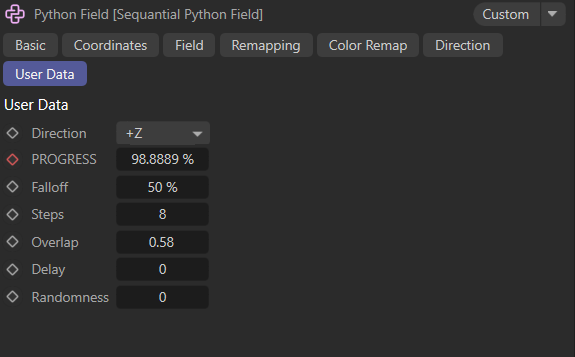
- Add the custom User Data sliders:
- Direction
- Progress
- Falloff
- Steps
- Overlap
- Delay
- Randomness
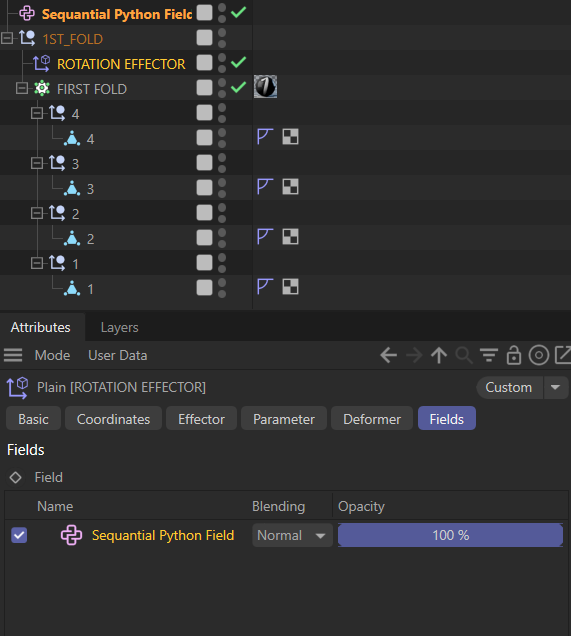
- Drag the Python Field into an Effector, Deformer, or Weight system.
- Animate the Progress slider to reveal clones in order.
You get a fully controllable, production-ready sequential animation tool.
Real Production Scenarios
Broadcast Packages
Reveal dozens of elements in a perfectly timed sequence, without worrying about their positions.
UI/UX Style Motion
Make interface modules appear exactly in the order you need, especially in futuristic HUD or holo-UI designs.
Logo or Icon Walls
Reveal hundreds of icons in cascading steps, waves, or patterns without timeline clutter.
3D Data Visualizations
Trigger clones in index order while their positions may be driven by external data sources.
Product Explainer Animations
Animate parts of a model assembling in logical steps, matching voiceover timing.
Conclusion
This sequential MoGraph Field becomes a creative Swiss-army knife for Cinema 4D motion designers.
It gives you order-based timing, clean control, and production-level flexibility, all while integrating seamlessly into existing MoGraph setups.
Whether you’re animating 20 clones or 20,000, this tool unlocks a polished, art-directable animation style that would otherwise require complicated keyframing or Python rigging.
import c4d
from c4d.modules import mograph as mo
import math
import random
# User Data IDs
ID_DIRECTION = 1
ID_PROGRESS = 2
ID_FALLOFF = 3
ID_STEPS = 4
ID_OVERLAP = 5
ID_DELAY = 6
ID_RANDOMNESS = 7
DEBUG = True
def dbg(m):
if DEBUG: print(m)
def _read01(v, d=0.0):
if v is None: return d
v = float(v)
if v > 1.0: v /= 100.0
return max(0,min(1,v))
def _clamp01(x):
return max(0.0,min(1.0,x))
def Sample(op, inputs, outputs, info):
direction = op[c4d.ID_USERDATA, ID_DIRECTION]
progress = _read01(op[c4d.ID_USERDATA, ID_PROGRESS], 0.0)
falloff = _read01(op[c4d.ID_USERDATA, ID_FALLOFF], 0.2)
steps = int(op[c4d.ID_USERDATA, ID_STEPS] or 1)
overlap = _read01(op[c4d.ID_USERDATA, ID_OVERLAP], 0.0)
delay = _read01(op[c4d.ID_USERDATA, ID_DELAY], 0.0)
randomness = _read01(op[c4d.ID_USERDATA, ID_RANDOMNESS], 0.0)
if steps < 1: steps = 1
if not inputs._position: return False
pts = inputs._position
n = len(pts)
# Sequential model ignores world positions.
# Sweep runs from clone 0 → clone n-1.
# Each clone has a "sweep coordinate" based purely on order.
if n == 0:
outputs._value = []
return True
# Axis selection for consistent behavior (used only for direction sign)
signs = [1,-1,1,-1,1,-1]
if direction is None or direction < 0 or direction > 5:
direction = 0
dir_sign = signs[direction]
# TOTAL SWEEP normalized to [0..1] across clone indices
# Each clone is at u = i/(n-1)
def index_to_u(i):
if n<=1: return 0.0
return i/float(n-1)
# world-falloff replaced with sequential-falloff in normalized units
seq_falloff = falloff
if seq_falloff <= 1e-6: seq_falloff = 1e-6
half_f = seq_falloff*0.5
# randomness (timing jitter)
progress_factor = 1 - abs(progress*2 - 1) # max at 0.5
eff_rand = randomness * progress_factor
randoff = []
for i in range(n):
random.seed(i+1000)
randoff.append((random.random()-0.5) * eff_rand)
# Per-clone delay affects internal timeline
max_start = delay * max(0,n-1)
internal_total = 1.0 + max_start
t_int = progress * internal_total
# CONTINUOUS mode
if steps == 1:
out = []
for i in range(n):
u = index_to_u(i)
t0 = i*delay + randoff[i]
local = _clamp01(t_int - t0)
plane = -half_f*dir_sign + (1+half_f)*dir_sign * local
dist = (u*dir_sign) - plane
if dist <= -half_f: val = 1.0
elif dist >= half_f: val = 0.0
else:
t = (dist/(2*half_f)) + 0.5
t = _clamp01(t)
s = t*t*(3-2*t)
val = 1.0 - s
out.append(val)
outputs._value = out
outputs.ClearDeactivated(False)
return True
# STEPPED MODE
gap = 1.0-overlap
gap = max(0,min(1,gap))
span = (steps-1)*gap + 1.0
out = []
eps = 1e-9
for i in range(n):
u = index_to_u(i)
t0 = i*delay + randoff[i]
local = _clamp01(t_int - t0)
ip_eff = local * span
uf = u * steps
part = int(math.floor(uf))
if abs(uf - round(uf)) < eps:
k = int(round(uf))
if k>0 and k<steps: part = k-1
else: part = min(max(k,0), steps-1)
else:
part = min(max(part,0), steps-1)
seg_start = part/steps
seg_end = (part+1)/steps
plane_start = seg_start - half_f*dir_sign
plane_end = seg_end + half_f*dir_sign
s_i = part * gap
e_i = s_i + 1.0
if ip_eff <= s_i: tp = 0.0
elif ip_eff >= e_i: tp = 1.0
else: tp = (ip_eff - s_i)/(e_i - s_i)
plane = plane_start + (plane_end-plane_start)*tp
dist = (u*dir_sign) - plane
if dist <= -half_f: val = 1.0
elif dist >= half_f: val = 0.0
else:
t = (dist/(2*half_f))+0.5
t = _clamp01(t)
s = t*t*(3-2*t)
val = 1.0 - s
out.append(val)
outputs._value = out
outputs.ClearDeactivated(False)
return True